

電機是一種電磁裝置,其核心主要由繞組線圈和鐵心等電磁部件組成,既然有線圈和鐵心,就必然繞不開電感的問題。經常有同學張口閉口電機的電感如何如何,殊不知電機中的電感那講究大了去了,自感、互感、相電感、線電感、直軸電感、交軸電感、主電感、漏電感、瞬態電感(電抗)、超瞬態電感(電抗)…這些令人眼花繚亂的電感都是怎么定義的?其物理意義又是啥?各種電感之間的關系是什么?這些電感怎么測量、怎么使用?本期就詳細說說電機中電感的那些事。
一、什么叫電感
說起“電感”,通常有兩個含義:一是指一種帶有線圈的電磁器件,也稱電感器或電抗器;二是指線圈固有的一種電氣參數,通常用“L”表示,其單位為:亨利(簡稱亨H)、毫亨(mH)、微亨(μH)等,我們這里所說的電感是指后者,線圈的電感又有自感和互感之分,單個線圈只有自感,多個線圈除了各自有自感外,如果它們的磁路之間存在相互聯系,還會有互感之說。
1、單個線圈的自感
自感是描述單個線圈通以電流時產生磁場(磁通)能力的物理量。由物理知識可知,一個線圈通以電流時會在其周圍產生磁場,通常用磁力線來描述其周圍的磁場,如圖1所示。
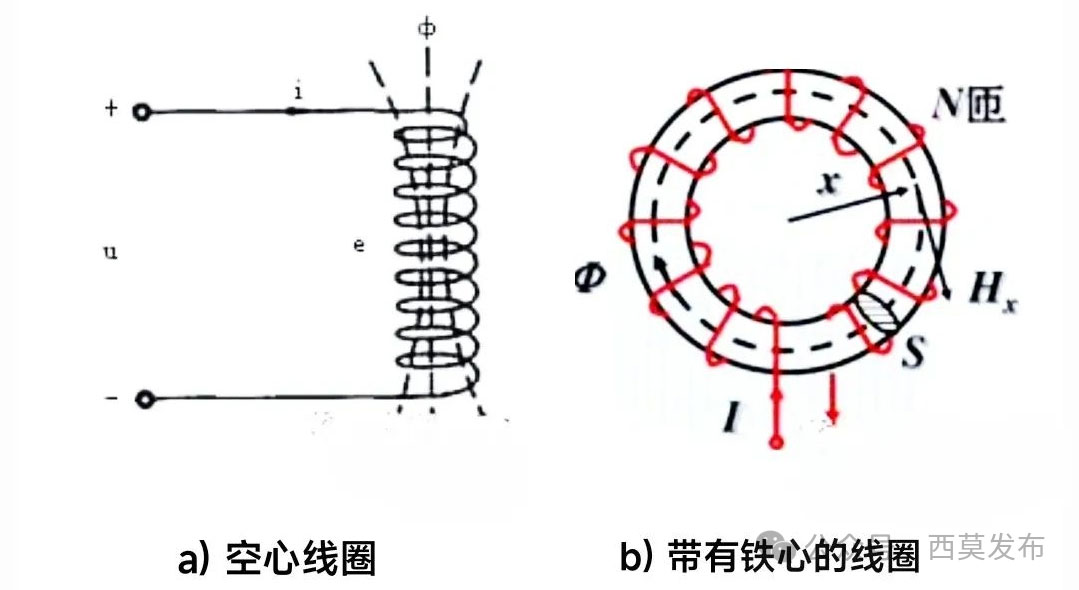
圖1 線圈的自感
定義:線圈通以單位電流時產生的匝鏈線圈本身的磁鏈稱為該線圈的自感,用L表示,即:
L=ψ/i ⑴
式中:L為線圈的自感(H);i為線圈中所通的電流(A),ψ為通電后線圈產生的匝鏈線圈本身的磁鏈(Wb),ψ=ΦN;Φ為磁通量;N為線圈匝數。通俗地講就是給線圈通1A的電流能產生“幾根磁力線”就叫線圈的自感是多少。式⑴被稱為自感的定義式,常用該式來測定線圈的自感。
雖然線圈的自感如⑴式所示等于磁鏈除以電流,但自感的大小卻與線圈是否通電流以及通電流大小無關(忽略磁飽和因素)。這就像一段導體的電阻R=U/I一樣,雖然導體的電阻等于導體兩端的電壓除以導體中的電流,但一段導體的電阻大小卻與是否通電以及通多大電流無關,導體的電阻只與導體的粗細、導體長度以及導體的材料有關,一段導體即使不通電,它的電阻該是多少還是多少,也就是說,導體的電阻是這段導體的一個固有參數,其大小只取決于這段導體的固有結構和材料。同理,線圈的自感也是線圈的固有參數,一個線圈繞制完成后,其自感就確定了,決定線圈自感大小的是線圈本身的固有結構。那么決定自感大小的因素有哪些呢?首先,線圈的自感與線圈的匝數有關,同樣通1A的電流,繞兩圈的線圈就比繞一圈的線圈產生的磁通量大,因此繞兩圈的線圈就比繞一圈的自感大;其次,線圈的自感還與線圈磁路的磁導(磁阻)有關,也就是說,同樣匝數和形狀的線圈,如果是空心的,如圖1a)所示,由于空氣的磁導率很小,通1A電流產生的磁通就很少;如果把線圈繞在鐵芯上,如圖1b)所示,由于鐵的磁導率遠高于空氣,同樣通1A的電流產生的磁通就會多出許多倍,因此同樣匝數和形狀的線圈,帶鐵心的比不帶鐵心的自感要大許多倍。
當線圈的結構一定時,其自感為:
L=N2Λ ⑵
式⑵被稱為線圈自感的決定式,它表明線圈的自感是由線圈本身的固有結構決定的,式中:N為線圈的匝數;Λ為磁路的磁導:
Λ=μ·S/l? ⑶
式中:μ為磁路材料的磁導率,S為磁路的截面積,l為磁路長度。
2、初始電感、視在電感、增量電感
對于空心線圈,由于空氣的磁導率為一常數,因此線圈的自感也是一個常數,人們常把空心線圈也叫做線性電感;對于有鐵心的線圈,由于鐵心存在磁飽和問題,鐵心材料飽和后磁導率不再是個常數,因此線圈的自感也不再是一個常數,會和線圈所通電流大小有關,為此,需要把帶有鐵心的線圈自感進一步細分。如圖2所示,為一帶有鐵心的線圈通電流時所產生的磁鏈與所通電流的關系曲線,其實就是鐵心的磁化曲線。
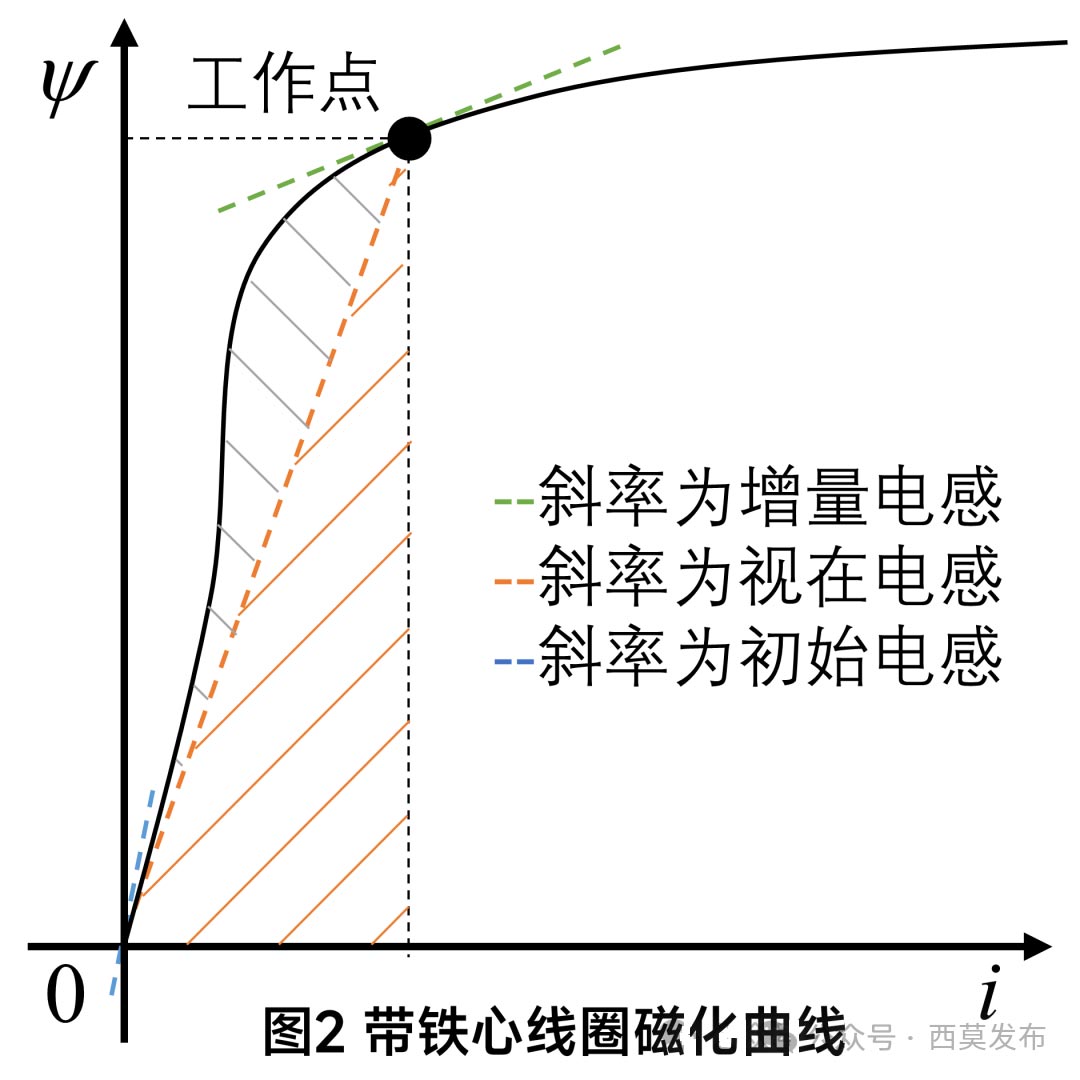
由圖2和式⑴可知,當所通電流較小時,鐵心不飽和,曲線近似為一直線,工作點的磁鏈與電流之比(ψ/i)近似為一常數,即自感可看作一個常數,我們將這一線性段的電感稱為初始電感,也稱為線圈電感的不飽和值,其大小為曲線初始段的斜率;隨著電流的增大,鐵心出現飽和現象,此時工作點的磁鏈與電流之比(ψ/i)不再是一個常數,意味著飽和后線圈的自感不再是一個常數,而是隨著工作點的變化而變化,我們將此時的電感稱為視在電感,由于飽和后工作點到原點的線段為磁化曲線的割線,視在電感(ψ/i)就是割線的斜率,因此視在電感也被稱為割線電感。顯然視在電感的大小與工作點的飽和程度有關,因此視在電感還被稱為線圈自感的飽和值。除了上述兩種電感外,還經常用到增量電感,所謂增量電感是指工作點處的增量磁鏈與增量電流之比(dψ/di) ,即磁化曲線上工作點處的切線斜率,因此增量電感也被稱為切線電感。從各種電感的定義及圖2可知,曲線初始階段為直線,因此初始電感、視在電感、增量電感沒有什么區別,在曲線膝點之前的線性區域可以近似認為視在電感與增量電感基本一致;隨著飽和程度增加,增量電感和視在電感都會有所減小,當鐵心達到深度飽和后,增量電感又趨近于一個常數。
電機繞組的視在電感常被用來分析電機的穩態特性,而增量電感常用來分析電機的動態性能,在電機控制中會經常用到。
3、線圈之間的互感?
如果兩個線圈共用一個磁路或兩個線圈的磁路存在聯系,其中一個線圈通以電流時,產生的磁通除了匝鏈本線圈外還匝鏈另一個線圈,那么這兩個線圈除了各自存在自感外,它們之間還存在互感,如圖3所示。
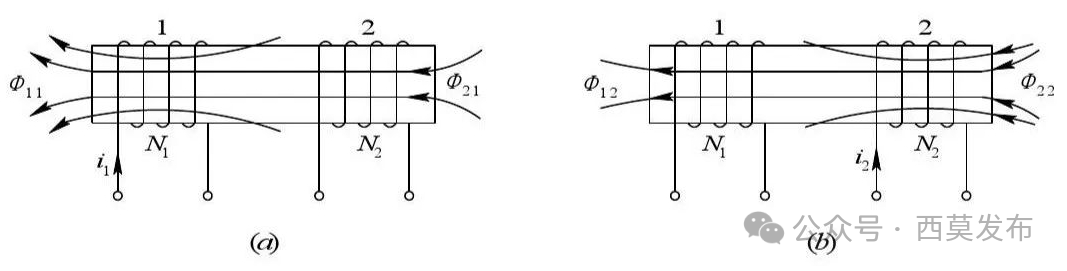
圖3 兩個線圈的互感
定義:在線圈1中通以單位電流產生的匝鏈于線圈2的磁鏈叫做線圈1對線圈2的互感,即L??=ψ??/i?;同理,線圈2對線圈1的互感為L??=ψ??/i?。理論和實踐都表明:兩線圈之間的互感大小取決于兩個線圈兩線圈的固有結構和相對位置,當兩線圈的結構和相對位置一定時,它們之間的互感是可逆的,即:L??=L??。
4、線圈串并聯時的等效電感
如果兩個獨立的線圈L?和L?,它們之間不存在互感,那么這兩個電感線圈串聯后的總電感就等于兩個電感之和,即:L=L?+L?;這兩個電感線圈并聯后的總電感就等于兩個電感之乘積除以兩個電感之和,即:L=L?L?/(L?+L?),這一點和電阻的串并聯規律是一樣的。如果兩個電感之間存在互感M,那么它們串并聯后的總電感就遠不像上面說的那么簡單了,篇幅所限,我們這里只說結果,有關推導可自行參見物理或電工學相關文獻。如圖4所示為相互之間存在互感的兩個線圈串聯和并聯的電路,其中:圖4a)為兩個存在互感的線圈正向串聯(兩個線圈的同名端順串);圖4b)為兩個存在互感的線圈反向串聯(兩個線圈的同名端反串);圖4c)為兩個存在互感的線圈正向并聯;圖4d)為兩個存在互感的線圈反向并聯。
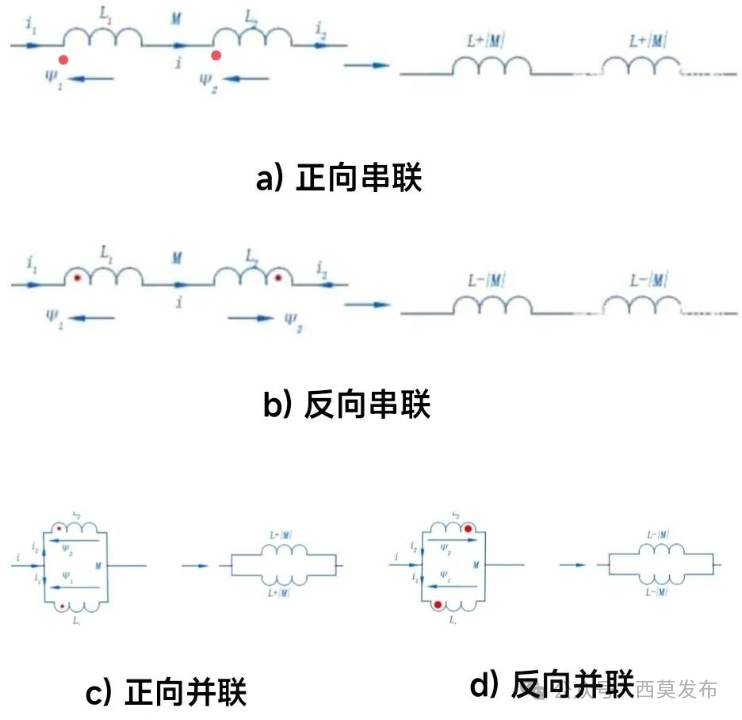
圖4 兩線圈存在互感時的串并聯電路
對于圖4a)和圖4b)所示的串聯電路,兩個線圈串聯后的等效電感為:
L=L?+L?±2M ⑷
式中的“±”號對于圖4a)正向串聯時取“+”;對于圖4b)反向串聯時取“-”。
對于圖4c)和圖4d)所示的并聯電路,兩個線圈并聯后的等效電感為:
L=(L?L?-M2)/(L?+L??2M) ⑸
式中的“?”號對于圖4c)正向并聯時取“-”;對于圖4d)反向并聯時取“+”。
復習完以上基本物理概念,接下來分析電機繞組的各種電感。
二、電機繞組的電感
1、轉子對稱時電樞繞組的電感
電機分交流電機和直流電機兩種,這里僅分析交流電機的繞組電感。交流電機又分為同步電機和異步電機兩種,無論是同步電機還是異步電機,其電樞繞組的結構都是一樣的,電樞繞組通常為三相對稱繞組,嵌裝于定子側,同步電機和異步電機的區別在于轉子,異步電機的轉子是一個圓柱形狀的鐵心內嵌裝有三相對稱繞組(繞線式)或籠型繞組(鼠籠式)。而同步電機的轉子結構則種類繁多:有些嵌裝有勵磁繞組和阻尼繞組,稱為電勵磁同步電機;有些是裝有永磁體用于勵磁,稱為永磁同步電機;還有些則是通過轉子鐵心的非對稱形狀形成非對稱磁阻來產生電磁轉矩,稱為磁阻同步電機;除此之外還有些永磁電機,即可產生永磁轉矩還可產生磁阻轉矩,稱為內嵌式永磁同步電機(IPM);還有些同步電機轉子上即有勵磁繞組又有永磁體,稱為混合勵磁同步電機。對于不同轉子結構的交流電機,其定子繞組的電感特性是不同的,我們首先來分析對稱轉子的交流電機電樞繞組電感。
所謂對稱轉子,是指轉子沿徑向各個方向上磁阻相等,電機的主磁路磁阻與轉子的位置無關,如:異步電機轉子、隱極同步電機轉子以及表貼式永磁同步電機的轉子均可看作對稱轉子,如圖5所示。
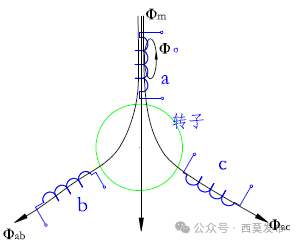
對于圖5所示的對稱轉子電機,由于三相定子繞組的匝數相同,三相繞組軸線互差120°空間電角度,且各相繞組的磁路磁導與轉子位置無關,因此,在忽略鐵心飽和的情況下,各相繞組的自感均相等,且為常數;任意兩相繞組之間的互感也相等,且為常數。
如果單獨給某一相繞組(以A相為例)通入電流I?,產生匝鏈A相繞組自身的磁鏈為ψ??;產生匝鏈B相繞組的磁鏈為ψ??;產生匝鏈C相繞組的磁鏈為ψ??。將匝鏈A相繞組的磁鏈ψ??分為漏磁鏈ψσ和穿越氣隙的電樞反應磁鏈ψ?兩部分,即:ψ??=ψσ+ψ?。則由于B相繞組和C相繞組與A相繞組在空間上差120°電角度,故ψ??=ψ??=-(1/2)ψ?。根據電感的定義,各相繞組的自感及相互之間的互感分別為:
L??=L??=L??=(ψσ+ψ?)/I?=ψσ/I?+ψ?/I?=Lσ+L?
L??=L??=L??=-(1/2)ψ?/I?=-(1/2)L? ⑹
式中:Lσ=ψσ/I?,為一相繞組的漏電感;L?=ψ?/I?,為一相繞組的電樞反應電感。
雖然根據⑹式可以得出三相繞組獨立的自感和相互之間的互感,但在對稱轉子的電機中,這些獨立的電感參數并不常見,特別是在電機的穩態分析時,這些獨立的電感參數意義并不大,只是在動態建模分析時才會用到。在異步電機、隱極同步電機等對稱轉子電機進行穩態分析時,通常采用三相繞組聯合作用的電感(抗)參數來進行分析計算,推導等效電路,因此對于對稱轉子的電機,三相繞組聯合作用下的電感參數更為常見,也更有意義。
如果在三相繞組中通入三相對稱交流電流,就會在氣隙中產生應該圓形的旋轉磁場,同時在每相繞組中還會產生一定的交變漏磁。設三相繞組所通三相對稱交流電流的幅值為Im,所產生的旋轉磁場的每極主磁通為Φm,每相漏磁鏈為ψσ。由于每極主磁通Φm是三相繞組聯合產生的,考慮到三相繞組之間互感,因此Φm應該是一相繞組單獨通電產生的磁通Φ?的1.5倍,即Φm=1.5Φ?。主磁通Φm在旋轉過程中會依次匝鏈各相繞組,從而在各相繞組中產生交變的磁鏈,交變磁鏈的最大值為ψm=1.5ψ?,根據電感的定義,各相繞組的電感為:
L?=L?=L?=(ψm+ψσ)/Im=ψm/Im+ψσ/Im=ψσ/Im+1.5ψ?/Im=Lσ+1.5L?=Lσ+Lm ⑺
式中:Lσ=ψσ/Im為漏電感;Lm=ψm/Im=1.5L?為電機的主電感。在異步電機中Lm通常被稱為激磁電感,對應異步電機等效電路中的激磁電抗;在隱極同步電機中Lm通常被稱為電樞反應電感,對應隱極同步電機等效電路中的電樞反應電抗,主電感Lm與漏電感Lσ之和稱為同步電感,對應同步電抗。
再次強調,上述根據電感定義求取各電感時,ψm并不是只針對某一相繞組通電流產生的磁鏈,而是三相繞組通入三相電流聯合作用產生的磁鏈,與之相除的電流也不是某一相繞組的電流,而是三相繞組同時所通的三相電流的最大值,這就意味著⑺式中的各相繞組的電感是考慮了三相繞組之間的互感影響而得到的綜合電感,也稱主電感。這種考慮了三相繞組聯合作用的效果得到的參數在電機學中稱之為“三相系統”下的參數,這是有別于單個或多個獨立線圈自感和互感參數的重要差別,如無特別說明,三相電機的電感參數都是指“三相系統”下參數(后續同)。
2、轉子非對稱時電樞繞組的電感?
當轉子各向磁導不對稱(dq軸磁導不相等)時,稱為非對稱轉子,如凸極同步電機和內嵌式永磁電機轉子、磁阻同步電機轉子等,由于繞組磁路的磁導與轉子位置有關,所以各相繞組的自感和互感就成為了轉子位置的函數,我們以電勵磁凸極同步電機為例介紹轉子非對稱時電樞繞組的電感,如圖6所示。
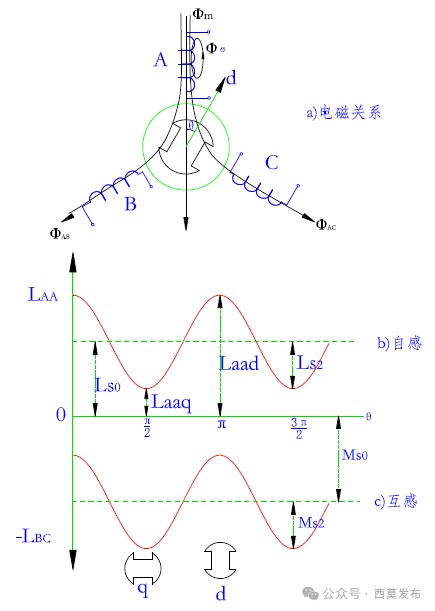
圖6 轉子非對稱時電樞繞組的自感和互感
由圖6可見,當轉子直軸(d軸)對齊A相繞組軸線時,A相繞組的磁阻最小,如果此時給A相繞組單獨通電流,產生的磁通最大,說明此時A相繞組自感最大;如果此時給B相繞組通電流,產生的匝鏈于C相繞組的磁通最小,說明此時BC相繞組之間的互感絕對值最小,設三相繞組的同名端都取繞組的首端,則三相繞組之間的互感實際值均為負值。同理,當轉子交軸(q軸)對齊A相繞組軸線時,A相繞組自感最小,而BC相繞組之間的互感絕對值最大。隨著轉子位置的不同,自感和互感分別以一個恒定的平均值Ls?和Ms?為中心呈二倍頻余弦規律波動,波動的幅度分別為Ls?和Ms?,如圖6b)、圖6c)所示,各相繞組的自感和互感為:
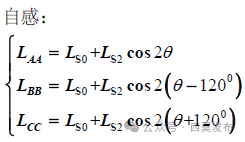
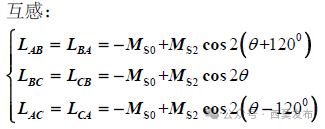
式中:
Ls?=Lσ+(Laad+Laaq)/2
Ls?=(Laad-Laaq)/2
Ms?=Mσ+(Laad+Laaq)/4
Ms?=(Laad-Laaq)/2
Lσ和Mσ分別為漏自感和漏互感;Laad和Laaq分別稱為直軸和交軸對齊某相軸線時,該相繞組的電樞反應電感。
需要特別說明的是,上述⑻式和⑼式中的電感參數均為三相繞組各自獨立的參數,并不是前面所說的“三相系統”下的參數。也就是說⑻式和⑼式中的自感和互感參數是指單獨給某一相繞組通電時得到的自感和互感,并沒有考慮三相繞組同時通電的聯合作用效果。
3、直軸電感和交軸電感?
以上討論的是在定子abc坐標系下各相繞組的自感和它們之間的互感,其物理意義較為直觀,各電感值就是實際繞組的電感值。
對于異步電機這樣的各向均勻對稱的轉子,各相繞組的自感及互感均為常數,因此異步機可以得到一個以恒定繞組參數組成的等效電路。但對于同步電機而言,其繞組電感參數與轉子位置有關,是轉子位置角θ的函數,當轉子旋轉時θ就是時間的函數,因此繞組的自感和互感也就是時間的函數。雖然這些參數都是實際繞組的物理實際值,但由于參數隨時間變化,用這些時變參數來分析電機的性能及各種方程式十分繁雜,為了簡化同步電機的分析計算,需要轉化為恒定的繞組參數,為此對于凸極同步電機,通常采用“雙反應理論”進行分析。我們知道,三相對稱繞組中通以三相對稱交流電流時,會產生一個圓形的旋轉磁勢,而兩個以同步轉速旋轉的正交的兩相繞組中分別通以直流電流同樣可以產生一個圓形的旋轉磁勢,這就為“雙反應理論”奠定了基礎。所謂“雙反應理論”,就是把三相電樞繞組等效為兩個正交的同步旋轉繞組,其中一個繞組的軸線始終與d軸對齊,稱之為d軸繞組;另一個繞組的軸線始終與q軸對齊,稱之為q軸繞組。等效變換的原則是變換后dq繞組產生的旋轉磁勢等于原來三相繞組聯合作用產生的旋轉總磁勢,只有這樣才能保證變換前后電機內部的電磁關系和能量轉換關系不變。通常有兩種等效方法:一種是所謂的“等幅值變換”,即變換前后兩種繞組中的電流、電壓、磁鏈幅值相等,這種等效方法會導致用dq兩相繞組計算出的功率與三相繞組計算出的功率不相等,在計算功率時需要乘以一個變換系數;另一種是所謂的“等功率變換”,即變換前后兩種繞組的功率相等,當然這種變換前后的電流、電壓、磁鏈幅值不相等。這兩種等效變換方法分別適用于不同的場合,這里默認采用等幅值變換。這種等效變換其實就是一種坐標變換,首先把原來靜止的abc坐標系下的三相電壓、電流、磁鏈等物理量變換成靜止的正交αβ坐標系下的兩相繞組的物理量,使α軸線與a相軸線重合,β軸超前α軸90°,這一變換稱為Clark變換(即3s→2s變換),當然也可以把靜止的兩相坐標變換回靜止三相坐標,即Clark逆變換(2s→3s變換);然后再將靜止的αβ坐標系下的各物理量變換為與轉子上的dq旋轉坐標系下的各物理量,d軸始終與轉子N極中心線重合,q軸超前d軸90°,這一步變換就是通常所說的Park變換(即2s→2r),當然也存在Clark逆變換(2r→2s變換)。
等幅值Clark變換的變換公式(轉換矩陣)為:

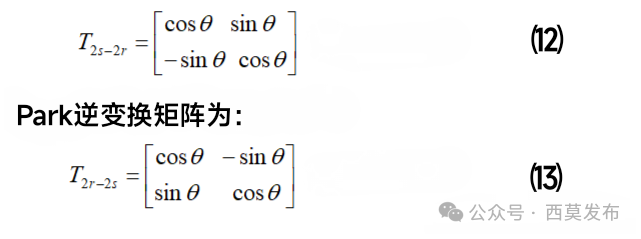
用上述轉換矩陣可以實現電壓、電流和磁鏈在不同坐標系下的轉換,上述變換矩陣的推導過程可參見相關文獻,篇幅所限在此不贅述。在原來靜止的abc坐標系下,三相繞組的自感和互感都是轉子位置的函數,如⑻式和⑼式所示,如果轉子旋轉,這些電感參數就是時變函數,非常復雜,難以計算分析,經過以上變換后,由于dq軸繞組隨轉子同步旋轉,使得原來的三相繞組中的交流電壓、電流和磁鏈變換成為dq繞組中的恒值電壓、電流和磁鏈的直流量,電感也由原來隨轉子位置變化的量變成了恒定量,而且由于dq軸相互垂直,因此dq繞組間也不存在互感了。三相繞組電感變換為旋轉dq軸繞組電感的公式為(推導過程略):
![]()
雖然按⒁式可以求出dq坐標系下的直軸電感Ld和交軸電感Lq,但求解過程的非常繁瑣,而且不能體現交直軸電感的物理意義,純屬一種數學推導過程,為此我們還是從物理意義上對交直軸電感予以推導。根據繞組電感的定義,d軸繞組的電感Ld即為在d軸繞組中通1A的電流時所產生的磁鏈,即Ld=ψd/Id;q軸繞組的電感Lq即為在q軸繞組中通1A的電流時所產生的磁鏈,即Lq=ψq/Iq。由于Ld和Lq均是一個恒值,不再與轉子位置有關,我們就不妨在轉子d軸對齊A相軸線(θ=0°)時,給d軸通入Id=Im的電流,q軸內不通電流(Iq=0),此時d軸繞組產生的磁鏈為ψm,根據坐標變換等效原則,ψm應該與A相電流的瞬時值達到峰值(i?=Im)、其余兩相電流均為負的一半峰值(i?=i?=-0.5Im)時三相繞組聯合產生的磁鏈相等,即:
ψm=Ld*Id=Ld*Im=L??(0°)*Im+L??(0°)*(-0.5Im)+L??(0°)*(-0.5Im)=[Lσ+ Mσ +(3/2)Laad]Im ⒂
由⒂式得直軸電感:
Ld=Lσ+ Mσ +(3/2)Laad=Lσ +Mσ + Lad ⒃
同理,如果我們在q軸對齊A相相軸(θ=90°)時,給交軸繞組通電流,直軸不通電流(Id=0、Iq=Im),則q軸繞組產生的磁鏈ψm應該等于q軸對齊A相繞組軸線(θ=90°)時,A相電流達到峰值(i?=Im)、其余兩相電流均為負的一半峰值(i?=i?=-0.5Im)時三相繞組聯合產生的磁鏈,即:
ψm=Lq*Iq=Lq*Im=L??(90°)*Im+L??(90°)*(-0.5Im)+L??(90°)*(-0.5Im)=(Lσ+ Mσ +3Laaq/2)Im ⒄
由⒄式得交軸電感:
Lq=Lσ+ Mσ +(3/2)Laaq=Lσ +Mσ + Laq ⒅
式⒃和式⒅中:Lad和Laq分別為三相系統下的直軸電樞反應電感和交軸電樞反應電感,Lad=(3/2)Laad,Laq=(3/2)Laaq。由于d軸繞組和q軸繞組正交,因此二者之間不存在互感問題,即兩繞組互感為0。
綜上可見,經過以上變換,繞組的電感參數大為簡化,由原來的三相時變量電感變為了dq軸上的恒定量,但其物理意義被弱化了,為了便于理解,有必要再進一步說明一下交直軸電感的物理意義:由以上推導可知,直軸電感Ld其實就是當轉子d軸對齊某相繞組軸線時,該相繞組的自感;交軸電感Lq就是當轉子q軸對齊某相繞組軸線時,該相繞組的自感。當然由于交直軸電感是三相系統下的參數,考慮到原來三相繞組之間存在互感,三相繞組同時通電時,除了要考慮本相繞組通電產生的磁鏈,還要考慮另外兩相中的電流也會對該相繞組產生互感磁通,也就是把一相繞組的電樞反應電感Laad和Laaq放大3/2倍再加上其它兩相繞組的漏互感,才能得到與三相系統完全等效交直軸電感。?
4、相電感和線電感
經常有同學提到相電感、線電感。關于相電感,其實在前面的2.2節中已經講得很清楚了,所謂“相電感”就是各相繞組自己獨立的自感以及它們之間的互感,式⑻、式⑼和式⑹就是各相繞組的相電感,其中式⑻和式⑼對應非對稱轉子,由于非對稱轉子的磁導非對稱,因此繞組的相電感與轉子位置有關。如果是對稱轉子,則各相電感均為常數,與轉子位置無關,由此可見,式⑹可以看作是式⑻和式⑼的一個特例,按式⑻和式⑼只計算恒定部分Ls?和Ms?即可,不存在交變部分Ls?和Ms?。
所謂“線電感”就是在三相繞組的任意兩個出線端看進去的電感,因此“線電感”其實并不是某一相繞組的參數,而是多個繞組串并聯后的等效電感參數。我們首先看三相繞組Y型接法時的線電感,如圖7所示。
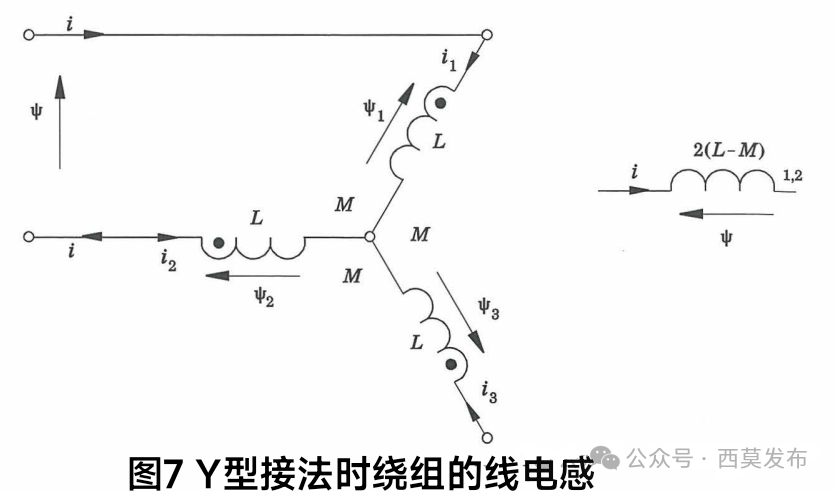
由圖7可以看出,Y型接法的繞組線電感其實就是兩相繞組反向串聯時的等效電感,根據式⑷可得Y型接法的繞組線電感為:
L??=2(L-M) ⒆
將⑻式和⑼式中相應的自感和互感代入⒆式,并整理得:
L??=2(Lσ + Mσ)+(3/2)[(Laad+Laaq)-(Laad-Laaq)cos2θ] ⒇
由⒇式可見,在非對稱轉子電機中,線電感也是隨轉子位置角θ變化的,隨著轉子位置的不同,線電感總存在一個最大值Lmax和一個最小值Lmin。
對于內嵌式永磁電機,通常Laad<Laaq,因此線電感的最大值和最小值分別為:
Lmax=2[(Lσ + Mσ)+(3/2)Laaq]=2Lq
Lmin=2[(Lσ + Mσ)+(3/2)Laad]=2Ld(21)
對于電勵磁同步電機,通常Laad>Laaq,因此線電感的最大值和最小值分別為:
Lmax=2[(Lσ + Mσ)+(3/2)Laad]=2Ld
Lmin=2[(Lσ + Mσ)+(3/2)Laaq]=2Lq (22)
對于三角形接法的繞組,線電感的等效電路如圖8所示。
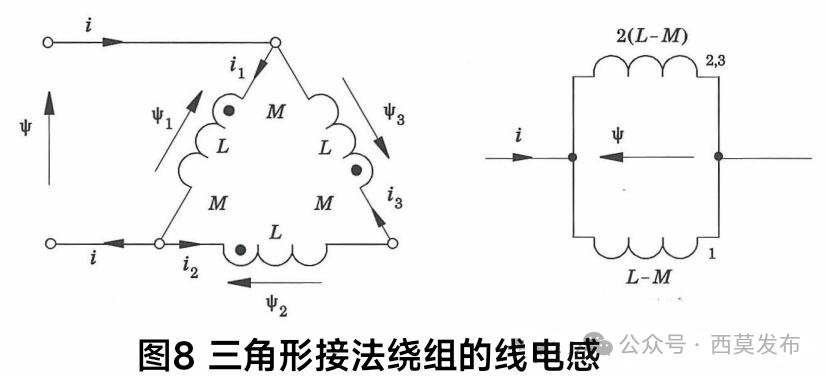
由圖8可知,三角形接法時繞組的線電感:
L??=(2/3)(L-M) (23)
將⑻式和⑼式中相應的自感和互感代入(23)式,并整理后(推導過程略)同樣會得到一個與轉子位置有關的線電感表達式,隨著轉子位置角θ的不同,同樣會有一個最大值Lmax和一個最小值Lmin,對于內嵌式永磁電機:
Lmax=(2/3)Lq
Lmin=(2/3)Ld(24)
對于電勵磁凸極同步電機:
Lmax=(2/3)Ld
Lmin=(2/3)Lq(25)
以上(21)、(22)、(24)、(25)各式反映了凸極同步電機線電感與交直軸電感之間關系,式(21)和式(22)適用于Y型接法的繞組,式(24)和式(25)適用于三角形接法的繞組。由于線電感往往比較容易測得的,因此可以利用這一關系來實測電機的交直軸電感。
5、電勵磁同步電機的瞬變電感和交超瞬變電感
在電勵磁同步電機中,轉子直軸上會布置有勵磁繞組,交直軸上還都布置有阻尼繞組,這些繞組都會與定子繞組存在互感。由電機學知識可知,如果把勵磁繞組和阻尼繞組都看作超導體繞組,那么這些超導繞組會產生阻止磁通穿越它的作用,這樣在瞬態時定子交直軸繞組產生的磁通會被迫排擠到漏磁路中,磁導大幅減小,此時交直軸繞組所反映出的電感遠小于穩態時的Ld、Lq,我們分別稱之為直軸超瞬變Ld″和交軸超瞬變電感Lq″;若只有直軸勵磁繞組為超導,阻尼繞組開路,則磁通可以穿越阻尼繞組卻無法穿越勵磁繞組,這樣直軸電感會小于直軸穩態電感Ld但大于直軸超瞬變電感Ld″,我們稱之為直軸瞬變電感記為Ld′,Ld″<Ld′<Ld;由于交軸上無勵磁繞組,故不存在交軸瞬變電感問題。?
三、電機繞組各種電感之間的關系及測試方法
以上介紹了交流電機電樞繞組的各種電感,小結一下:
對稱轉子的交流電機,無論是各繞組獨立的電感還是“三相系統”下的主電感都是恒定值,與轉子位置無關。在異步電機和隱極同步電機穩態分析時,常采用“三相系統”下的主電感(抗)參數,等效電路中的激磁電感(抗)和電樞反應電感(抗)都是指“三相系統”下的主電感(抗)參數。
非對稱轉子的交流電機,雖然有三相繞組獨立的自感和互感,但這些電感參數不是一個恒定值,而是隨轉子位置的不同而變化的值,如式⑻、式⑼所示,由于在電機旋轉時這些參數都是時變參數,極其繁雜,因此這些參數在穩態分析時并不常用,只是在系統動態仿真時偶有應用。在凸極電機穩態分析時,常采用雙反應理論來進行分析,因此必須經過一系列的坐標變換,得到直軸電感Ld和交軸電感Lq,需要說明的是,交直軸電感也是“三相系統”下的電感參數。關于交直軸電感參數與各相繞組獨立的自感和互感參數之間的關系見⒁、⒃、⒅式。
由于三相繞組是物理存在的實際繞組,它們的自感和互感雖然繁雜,但物理意義非常清晰,且都能夠通過實測的方法直接得到這些參數。而交直軸繞組由于不是實實在在物理存在的繞組,而是為了簡化分析在數學上虛構的繞組,因此直接測量交直軸電感比較困難。在工程實踐中,常通過采用測試線電感的方法來間接地得到交直軸電感。具體測試方法可以用RLC測試儀直接測量三相繞組的線電感,測量時緩慢轉動轉子,測得線電感的最大值和最小值,然后根據(21)、(22)、(24)、(25)各式中適應的電機類別計算出相應電機的交直軸電感。當然也可以采用在兩相繞組的出線端直接加適當的(低壓)工頻交流電壓,測量電流,然后用歐姆定律計算出線間電抗,得到線電感。
除了上述方法間接測量交直軸電感外,還可采用如圖9所示的接法間接測量交直軸電感。
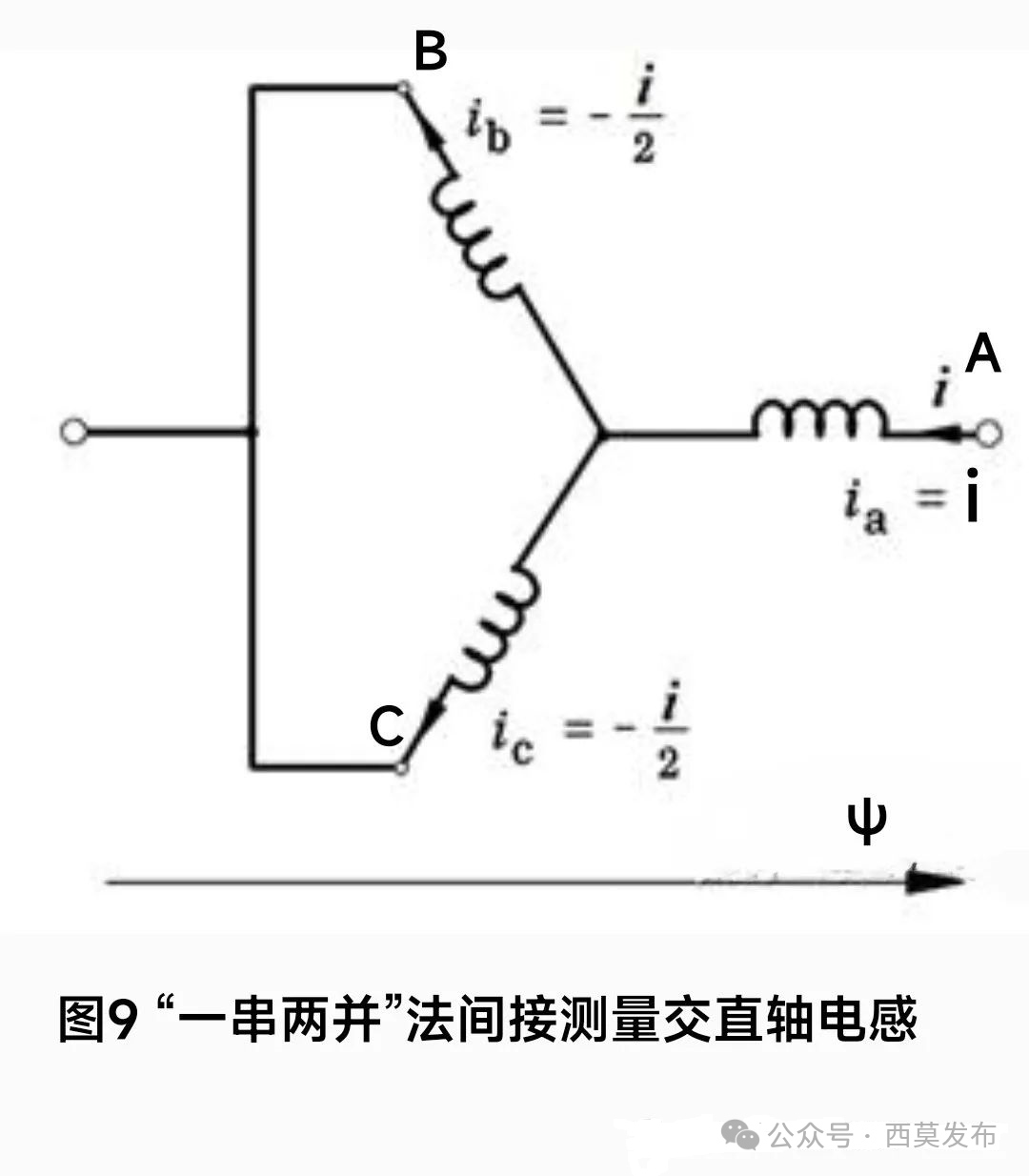
這種接法也稱為“一串兩并”接法,即將B、C兩相繞組并聯在一起,形成一個新的端點,用RLC測試儀或其他裝置測量該端點和A相繞組端點之間的電感。通過緩慢轉動轉子,同樣也可以測得一個電感的最大值Lmax和一個最小值Lmin,Lmax和Lmin與Ld和Lq的關系如下(推導過程略):
對于內嵌式的永磁同步電機
Lmax=(3/2)Lq
Lmin=(3/2)Ld (26)
對于電勵磁的凸極同步電機
Lmax=(3/2)Ld
Lmin=(3/2)Lq (27)
需要特別說明的是,上述測試方法,無論是用RLC測試儀還是加工頻交流電壓進行測試,本質上都是在繞組上施加了交流測試電源。對于永磁電機而言,這種測試方法測得的線電感是磁路工作點附近的切線電感;對于電勵磁同步電機,這種測試方法測得的線電感是不飽和值,這是因為測量時施加的電壓較低,磁路處于不飽和狀態,而且這種方法測得的線電感是超瞬變狀態下的線電感,因為對于交流電而言,轉子上的阻尼繞組會起到阻礙主磁通穿越阻尼繞組的作用,只有阻尼繞組開路時,這種方法測得的才是穩態交直軸電感,而對于一臺制造完成的電機,阻尼繞組不可能開路,因此對于有阻尼繞組的電勵磁同步電機不適合用這種測試方法來測試穩態交直軸電感,只能采取其它方法。關于交直軸電感的其它測試方法可參見GB/T1029,在此不贅述。
四、各種電感的用途
以上介紹了交流繞組的各種電感,它們各自都有什么用途呢?
首先,從宏觀上講,電機繞組的電感是電機的固有參數,決定著電機的各項主要性能,只有知道了這些電感,才能列寫出各種平衡方程式、得到電機的等效電路、分析電機的各種性能。
其次,電機控制需要知道這些電感參數,以便搭建準確的控制模型,進行精確控制。通常控制系統會根據電機的各種參數建立一個控制所需的數學模型,根據數學模型計算出所要控制量的給定值,通過與反饋量的比較得到差值,然后再通過PID或其它控制方法進行控制。這些電感參數可以由制造商在出廠試驗中測得,也可以通過控制軟件中自帶的參數自學習識別功能得到,為了更精確地實施控制,提高動態控制精度,對于非線性電感參數,有時需要采用狀態掃描的辦法事先對參數進行標定,得到不同運行狀態下的參數。
第三,在電機制造過程中,可以通過測量繞組的三相電感,通過其平衡性來判斷或診斷繞組的接線是否存在錯誤,是否存在電路方面的故障等。
第四,前面的介紹中講到電感參數有視在電感(割線電感)和增量電感(切線電感)之分,許多同學不清楚什么時候應該用視在電感,什么時候應該用增量電感。這要視具體情況,一般在做穩態分析時,通常用視在電感,而在做瞬態分析時,往往要用增量電感,特別是永磁電機的控制模型中,電感后面帶di時會用到增量電感。例如:內嵌式永磁電機的磁鏈為:
ψd=ψf+Ld*id
ψq=Lq*iq
以上兩式中的Ld和Lq就應該用視在電感,而永磁電機的電壓方程:
ud=id*R?+Ld*p(id)-ωLq*iq
uq=iq*R?+Lq*p(iq)+ω(ψf+Ld*id)
式中:p為微分算子,p=d/dt。以上兩式中p后面的Ld和Lq就應該用增量電感。
本文為西莫首席技術專家李保來老師(西莫ID:標準答案)原創文章,本期期刊西莫視角欄目收錄,并由西莫電子期刊主編hahafu整理發布以饗讀者。
AIP艾普專注全球測試,以上信息來源網絡,如有侵權請聯系作者更改。
 魯公網安備37021302000917號
魯公網安備37021302000917號